순차 탐색
탐색 과정
1. 원하는 값이 나올 때 까지 index를 증가시킨다.
2. 원하는 값을 찾으면 탐색을 중단한다.
시간 복잡도
평균 비교 횟수: (n+1)/2
최악 비교 횟수: n
시간 복잡도: O(n)
특징
1. 단순하다. (장점)
2. 비효율적이다. (단점)
이진 탐색
탐색 과정
0. 탐색할 배열이 오름차순(내림차순) 정렬이 되어있어야 한다.
1. 배열의 길이의 중간에 있는 값을 선택하여 탐색 하고자하는 값과 비교한다.
2. 해당 값이 탐색 하고자하는 값보다 크다면 우측으로, 작다면 좌측으로 이동하고 원하는 값을 탐색 할 때 까지 1-2번 과정을 반복한다.
더 이상 이동할 수 없어도(탐색할 후보군이 없어도) 탐색을 종료한다.
시간 복잡도
비교를 진행할 때마다 탐색 후보군이 절반으로 줄어든다. 따라서 N/2, N/4, ..., 1 로 진행할 때, 최종 탐색 후보군이 1개가 되도록 하려면 log2(n)번 이동해야한다.
최악 비교 횟수: log2(n)
시간 복잡도: O(logn)
특징
1. 탐색할 배열이 사전에 정렬되어 있어야한다.(단점)
2. 빠르다.(장점)
이진 트리 탐색
트리 구조란 그래프의 일종으로, 여러 노드가 한 노드를 가리킬 수 없는 구조이다. 간단하게는 회로가 없고, 서로 다른 두 노드를 잇는 길이 하나뿐인 그래프를 트리라고 부른다.
이진트리는 순회(탐색) 방법이 전위(Pre-order), 중위(In-order), 후위(Post-order), 레벨순서(Level-order, BFS) 총 3가지가 있다.
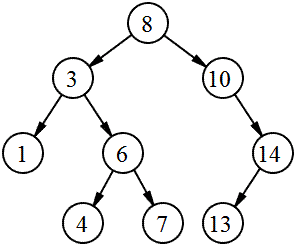
탐색 과정
전위(Pre-order): 8 3 1 6 4 7 10 14 13
방문 노드 탐색 -> 좌측 노드 방분 -> 우측 노드 방문
즉, 루트, 좌측, 우측 순으로 그리고 레벨이 낮을 수록 우선순위를 갖는다.
전위(In-order): 1 3 4 6 7 8 10 13 14
좌측 노드 방분 -> 방문 노드 탐색 -> 우측 노드 방문
즉, 좌측, 루트, 우측 순으로 그리고 레벨이 높을 수록 우선순위를 갖는다.
후위(Post-order): 1 4 7 6 3 13 14 10 8
좌측 노드 방분 -> 우측 노드 방문 -> 방문 노드 탐색
즉, 좌측, 우측, 루트 순으로 그리고 레벨이 낮을 수록 우선순위를 갖는다.
레벨순서(Level-order, BFS): 8 3 10 1 6 14 4 7 13
시간 복잡도
균형 상태:
n개의 자료들이 log2(n+1)의 높이를 가지므로 log2(n+1)의 비교안에 원하는 값을 탐색할 수 있다.
시간 복잡도: O(logn)
불균형 상태:
최악의 불균형 상태이면 n개의 자료들이 n의 높이를 가지므로 n번의 비교가 필요하다.
시간 복잡도: O(n)
특징
1. 우선 트리가 정렬되어 있어야한다.
2. 빠르다
힙 트리 탐색
힙(heap)은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리(complete binary tree)를 기본으로 한 자료구조(tree-based structure)로서 다음과 같은 힙 속성(property)을 만족한다.
- A가 B의 부모노드(parent node) 이면, A의 키(key)값과 B의 키값 사이에는 대소관계가 성립한다.
힙은 루트 노드에 최대/최소 값을 지니고 있고, 루트가 최대면 최대 힙(max heap), 루트가 최소면 최소 힙(min heap)이라고 부른다.
힙은 부모 노드와 자식노드 사이의 대소관계가 유지 되면서, 완전 이진 트리의 형태를 띄면 된다.
정 이진 트리(full binary tree): 모든 트리의 자식은 0개나 2개다.
포화 이진 트리(perfect binary tree): 모든 리프 노드의 높이가 같고 리프 노드가 아닌 노드는 모두 2개의 자식을 갖는다. 이진 트리에서 리프 높이의 최대치가 n일 때 가장 많이 존재할 수 있는 노드의 수는 2n-1개인데 포화 이진 트리는 이 개수를 모두 채운 이진 트리라고도 볼 수 있다. 또한, 모든 포화 이진 트리는 정 이진 트리이다.
완전 이진 트리(complete binary tree): 모든 리프노드의 높이가 최대 1 차이가 나고, 모든 노드의 오른쪽 자식이 있으면 왼쪽 자식이 있는 이진트리이다. 다시 말해 트리의 원소를 왼쪽에서 오른쪽으로 하나씩 빠짐없이 채워나간 형태이다. 포화 이진 트리는 완전 이진 트리의 부분집합이다. 단, 포화 이진 트리가 아닌 완전 이진 트리는 정 이진 트리일 수도 있고 아닐 수도 있다.
나무위키의 이진트리 종류 설명
완전 이진 트리의 형태를 띄는 이유는 삽입/삭제가 O(logn)으로 유지시키기 위해서이다.
탐색 과정
0. 최대힙은 최대값을, 최소힙은 최소값을 찾는다.
1. 최대힙이라면 최대값을, 최소힙이라면 최소값을 루트에 존재한다.
시간 복잡도
최대, 최소값은 루트에 늘 존재하기 때문에 O(1)의 시간에 찾을 수 있다.
이는, 원소의 삽입/삭제 시 O(logn)만큼의 시간을 소모하여 항상 루트의 값을 최대(최소)로 유지시키기 때문이다.
'Programming' 카테고리의 다른 글
| [알고리즘] 정렬(선택, 삽입, 퀵, 계수) (0) | 2022.05.10 |
|---|---|
| [Python] 실수하기 좋은 파이썬 문법들 (0) | 2022.03.05 |
| python-yeelight response error, Bulb closed the connection. 발생시 (0) | 2022.02.02 |
| [VSCode] Windows에서 remote-container vscode 붙이기 (0) | 2022.01.20 |
| [VSCode] vscode debugger 사용시 환경변수 세팅 (0) | 2022.01.18 |